R programming 비율 검정

• prop.test
• binom.test
• chisq.test
• fisher.test

---

prop.test

 

몇 가지 상황을 생각해봅시다.  

 

• 2번 중에서 1번 성공하면 확률은 0.5입니다. 
• 10번 중에서 5번 성공하면 확률은 0.5입니다. 
• 10번 중에서 5번 성공했는데, 사.실. 이 사건의 확률은 0.1 입니다. 

세 가지 경우 중에서 3번째는 뭔가 좀 이상하군요. 기존 확률에 비해서 너무 많이 성공했습니다. 

그럼 제가 0.1이라고 생각한 비율이 정말 맞는지 의심이 갑니다. 그래서 이게 얼마나 믿을만 한지 검정을 해봅시다. 

 

 

 2번 중에서 1번 성공하면 확률은 0.5입니다. 

prop.test(1, 2, 0.5) 

 

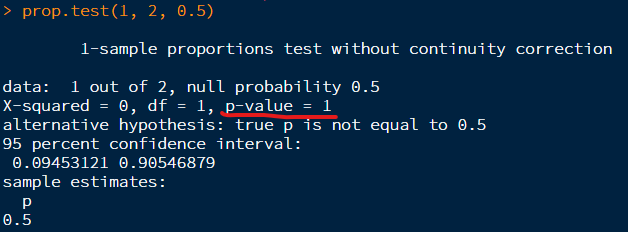
10번 중에서 5번 성공하면 확률은 0.5입니다. 

prop.test(1,10, 0.1)

 

10번 중에서 5번 성공했는데, 사.실. 이 사건의 확률은 0.1 입니다. 

p value 값이 기각될 정도로 작게 나왔습니다..

 

결론적으로 prop.test는 '성공/전체' 에 대하여 '내가 생각한 비율'이 얼마나 믿을만 한지 알려주는 테스트입니다.   

 

Quiz. 10번 중에 1번 성공한 경우와 100번 중에 10번 성공한 경우는 둘 다 비율이 0.1입니다. 

prop.test(1, 10, 0.5)
prop.test(10,100, 0.5) 

두 개의 P value는 다릅니다. 어떤 게 더 낮은 값을 가질까요?

 

---

binom.test

 

binom.test는 성공 실패로 나뉘는 binomal에서 왔습니다. 

사용법은 prop.test와 같고, 결과도 비슷합니다.  

 

prop.test(123,456, 0.3)  --> pvalue = 0.1741

binom.test(123,456, 0.3) --> pvalue = 0.1677

 

 

 

---

chisq.test

fisher.test

 

이번에는 조금 다른 경우를 생각해봅시다. 

 

A 학생 : 10번 중에 5번 성공했다.  --> 비율 0.5

B 학생 :   5번 중에 3번 성공했다.  --> 비율 0.6

 

두 학생에 대해서 비율은 상당히 유사해 보입니다. 

조금 문제를 바꿔봅시다. 

 

A 학생 : 100번 중에 53번 성공했다.  --> 비율 ..?

B 학생 :   23번 중에 15번 성공했다.  --> 비율 ..?

 

네.. 유사한 지 잘 모르겠습니다. 그래서 p-value에 의지해서 얼마나 다른지 알아보겠습니다 ^_^

일단 메트릭스를 만들어줍니다. 

 

 

mat <- matrix(c(53,13, 100-53, 23-13), 2)
혹은

mat <- matrix(c(53, 100-53, 13, 23-13), 2 ,byrow =T)

이 경우는 전체가 아닌 성공/실패를 기록합니다. 

 

 

chisq님께서 높은 pvalue로 두 비율이 유사하다고 하십니다. 

 

fisher님께서 높은 pvalue로 두 비율이 유사하다고 하십니다. 

 

전체 실행 코드

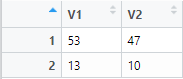
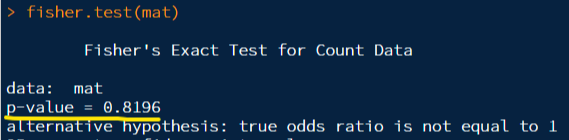
A 학생 : 100번 중에 53번 성공했다.  --> 비율 ..?

B 학생 :   23번 중에 15번 성공했다.  --> 비율 ..?

 

결론. chisq.test와 fisher.test 의 p-value가 높으므로  A, B 학생의 비율은 비슷하다. 

 

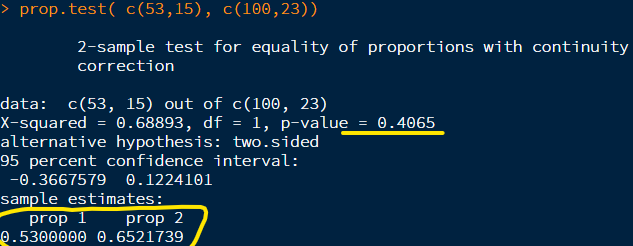
* prop.test( c(53,15), c(100,23)) 를 사용해도 됩니다. 

prop.test( c(53,15), c(100,23))