[차원축소][PCA의 원리] Principal component analysis

데이터 분석을 할 때, 컬럼의 수가 너무 많은 경우 차원을 줄여야 하는데 여러 기법들 중 하나인

PCA(Principle Componenet Analysis)의 원리에 대한 소개입니다. 

 

 

먼저 "Principle Component" 부터 살펴보겠습니다.

 

메트릭스 A 는 SVD(Single Value Decomposition)에 의해서 분해가 되는데,

시그마(아래 그림에서 핑크색)들로 나타낼 수 있습니다. 

수식은 몰라도 됩니다. 시그마(핑크색)을 이용해 저렇게 나타낼 수 있다는 사실이 중요합니다.

 

---

빠른 예시) 

시그마들이 항상 대각선인 건 아닙니다. 계산을 간단하게 하기 위해서 쉬운 메트릭스를 선택했습니다.

이 경우, 첫 번째 시그마 값인 9가 가장 큰 값을 차지하고 뒤로 갈수록 줄어듭니다. 

 

---

위의 예시를 가지고 계속 설명하면 약간의 변형을 통해서 다음 식을 얻습니다. 

 

여기서 U,V가 바로 Principle Componenet(주성분) 입니다. 

 

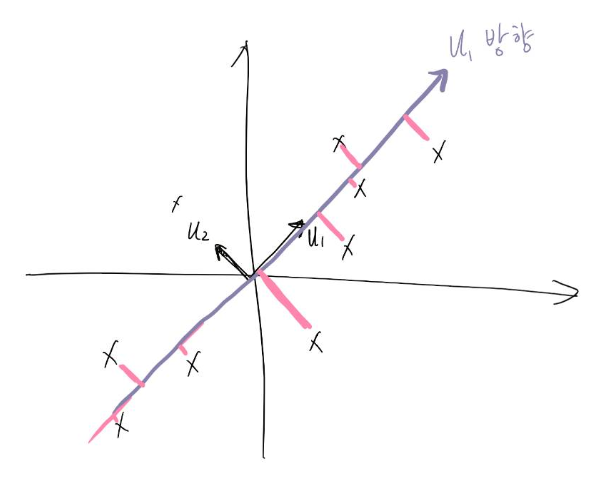
PCA를 하다보면 나오는 그래프에서 두 개의 방향이 위의 u1 u2가 되겠습니다. 

Principle component [출처 - 위키피디아]

u1에 대해서 시그마값이 가장 크기 때문에 기존 A 메트릭스의 가장 많은 부분을 설명할 수 있습니다. 

대학생의 스트레스 중에서 성적이 가장 큰 비중을 차지하는 것처럼

 

따라서 시그마가 가장 큰 2개의 방향 u1, u2를 가지고 

이렇게 적는다면 메트릭스를 가장 크게 보존하는 2가지 방향으로 차원을 축소한 게 됩니다. 

여기서 보존은 차이를 최소한으로 하는 방법을 말합니다.

---

2차원 --> 1차원으로 축소하는 예시

 

1. 데이터들이 주어졌을 때, 평균을 빼서 원점에 분포되도록 만들어 줍니다. 

2. SVD를 통해서 U, V, Sigma를 구합니다. 

3. U1방향으로 정사영합니다. 

 

2차원 데이터 --> 1차원 데이터.  X를 보라색 선으로 정사영시킨다. 핑크색은 차이를 나타냅니다.  

 

만일 u1이 아니라 임의의 방향에 대해서 축소를 시킨다면 차이가 커집니다.

파란색 선으로 차원을 축소했을 경우, 기존 보라색보다 차이가 심함

 

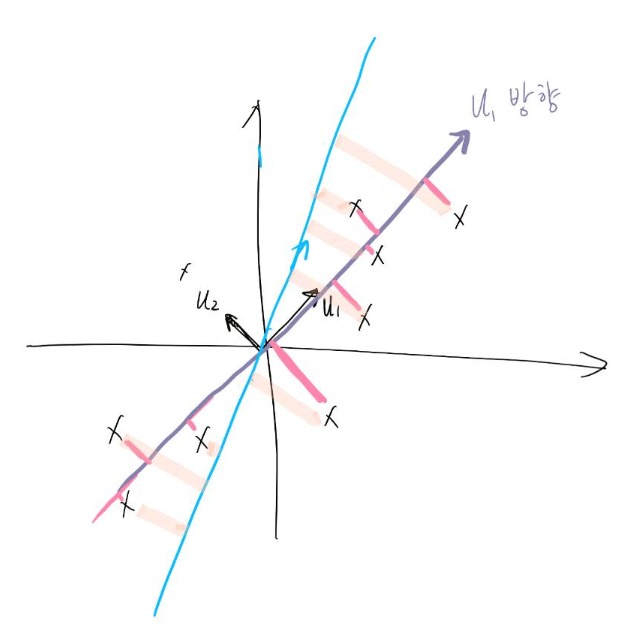
이에 대한 증명은 Eckart–Young–Mirsky theorem으로 할 수 있습니다.  

해석 : 임의의 k차원 메트릭스 중에 A와의 차이를 최소로 줄이는 메트릭스는 Ak이다. (Principal component이다.)

 

Eckart - Young 살펴보기 : https://en.wikipedia.org/wiki/Low-rank_approximation

Low-rank approximation - Wikipedia

Eckart - Young 강의 듣기 : https://ocw.mit.edu/courses/mathematics/18-065-matrix-methods-in-data-analysis-signal-processing-and-machine-learning-spring-2018/video-lectures/lecture-7-eckart-young-the-closest-rank-k-matrix-to-a/