Pytorch Autograd Case Study (create_graph for gradient and retrain_graph for multiple backwards)
🔥 Torch에는 🔖자동미분이라는 기능이 있어서, 미분을 우리가 굳이 하지 않아도 됩니다.
그런데 문제는 어떻게 동작하는지 모르니, 구현을 제대로 하기 쉽지 않습니다.
그래서 torch 에서 🔖autograd 가 사용되는 몇가지 use case 들을 정리하였습니다.

1. 단순히 High-order derivative 구하기
2. Neural Network 의 input 혹은 weight에 대해서 Gradient 구하기
3. Model-Agnostic Meta Learning (MAML) : 메터러닝
4. Hessian of a neural network (Hessian Vector Product)
5. Implicit Neural Representation
6. Multiple Backwards
---- 이외에 괜찮은 UseCase를 댓글로 소개해주시면 추가하겠습니다 🙂
---- 본문에서 사용된 코드 : https://github.com/fxnnxc/torch_autograd/blob/main/autograd_case_study.ipynb
---- Autograd 소개 (Pytorch) : https://tutorials.pytorch.kr/beginner/blitz/autograd_tutorial.html
---- 자동 미분 소개 (youtube) : https://www.youtube.com/watch?v=MswxJw-8PvE (강추)
1. 🔖 단순히 High-order derivative 구하기
가령 인풋 $x$에 대하여 함수값$f$ 의 미분계수를 구한다면, $\frac{d}{dx}$ 를 여러번 하여 계산할 수 있습니다.
$$\frac{df}{dx} ~~~~ \frac{d}{dx}\Big(\frac{df}{dx}\Big) ~~~~ \frac{d}{dx}\Big(\frac{d^2f}{dx^2}\Big)$$
이와 비슷하게 torch에서도 torch.autograd.grad(f, x, create_graph=True) 를 통하여 구한 Gradient 에 대해서 다시 Gradient를 구할 수 있습니다. 🔖create_graph 의 역할은 gradient 에 대해서도 computational graph를 만들어준 것입니다. 이로부터 구한 gradient는 gradient 를 저장할 수 있는 🔖Leaf (뒤가 없는 텐서) 가 되고, 이 값에 대해서 연산들 (제곱, 덧셈, 심지어 Gradient) 까지 계산할 수 있습니다.
import torch
v = -2.0
x = torch.tensor(v, requires_grad=True)
# function
f = 2 * x**3
print(f"x={v}, f = {f}")
# first order
f.backward(retain_graph=True) # 뒤에서도 다시 backward 를 해서 살려둡시다.
print(f"x={v}, df/dx = {x.grad}")
# second order
x.grad.zero_()
df = torch.autograd.grad(f, x, create_graph=True)[0]
df.backward(gradient=torch.tensor(1.0))
print(f"x={v}, d^2f/dx^2 = {x.grad}")
# thrid order
x.grad.zero_()
df = torch.autograd.grad(f, x, create_graph=True)[0]
ddf = torch.autograd.grad(df, x, create_graph=True)[0]
ddf.backward(gradient=torch.tensor(1.0))
print(f"x={v}, d^3f/dx^3 = {x.grad}")
해당 코드를 돌려보면, 아래와 같이 autograd로 구한 값과 수식으로 구한 값이 일치하는 것을 확인할 수 있습니다.

2. 🔖 Neural Network 의 input 혹은 weight에 대해서 Gradient 구하기
$f(x)$ 를 파라미터 $\theta$ 로 이루어진 Deep Neural Network 라고 한다면, Gradient 는 두 가지에 대해서 구할 수 있습니다.
1. input $x$ 에 대해서 $df/dx$
2. parameter $\theta$ 에 대해서 $df/d\theta$
혹은 심지어 파라미터에 대한 gradient 를 평균낸 값에 대해서도 구할 수 있습니다.
$$ G = \sum_\theta \Big(\frac{df}{d\theta} \Big)^2 $$
구현에서 한 가지 트릭은 🔖파라미터들을 일자로 만드는 것 입니다.
굳이 ([A,A,A], [B,B], [C], [D]) 레이어로 나눠져 있을 필요가 없이, [A,A,A,B,B,C,D] 형태로 만듭니다.
import torch.nn as nn
class Net(nn.Module):
def __init__(self):
super().__init__()
self.mlp = nn.Linear(2,5)
self.out = nn.Linear(5, 1)
def forward(self, x):
x = self.mlp(x**2)
x = nn.functional.relu(x)
x = self.out(x)
return x
net = Net()
input= torch.tensor([1.0]*2, requires_grad=True)
params = [p for p in net.parameters() if len(p.size()) > 1]
# gradient with respect to the input
print("------------ Gradient with respect to the input")
f = net(input)
f.backward()
print(input.grad)
# gradient with respect to the weights
print("------------ Gradient with respect to the weights")
input.grad.zero_()
f = net(input)
gx = torch.autograd.grad(f, params, create_graph=True)[0]
for i in range(2):
gx[i].sum().backward(retain_graph=True)
print(input.grad)
# gradient of weights to minimize the sum of squared of the gradients
print("------------ Gradients to the sum of squqared gradients")
net.zero_grad()
f = net(input)
gx = torch.autograd.grad(f, params, create_graph=True)[0]
(gx**2).sum().backward()
print([p.grad for p in params])
3. Model-Agnostic Meta Learning (MAML) : 메터러닝
다음 예시는 MAML에서 사용하는 Gradient Update 방식입니다.
MAML은 (1) meta-train 데이터에 대해서 weight를 계산하고, (2) meta-test 데이터에 대해서 update 된 weight를 최소화하는 방식으로 학습합니다. 이 때, (1) 에서 구한 weight는 $\theta' = \theta - \alpha \nabla_\theta L_{task} (f(\theta))$ 으로 구해지는데, gradient가 $\theta$ 에 대해서 파라미터로 계산됩니다. 이로부터 (2) 에서 다시 gradient 를 계산해줍니다.
$$ \theta \leftarrow \theta - \nabla_\theta L_{{meta}} (f(\theta')) $$
논문 : Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super().__init__()
self.mlp = nn.Linear(2,5)
self.out = nn.Linear(5, 1)
def forward(self, x, fast_weights=None):
if fast_weights is None:
x = self.mlp(x)
x = nn.functional.relu(x)
x = self.out(x)
else: # same logit with given weight
w, b = fast_weights[0], fast_weights[1]
x = F.linear(x, w, b)
x = nn.functional.relu(x)
w, b = fast_weights[2], fast_weights[3]
x = F.linear(x, w, b)
return x
net = Net()
lr=1e-3
meta_optim = torch.optim.Adam(net.parameters(), lr=lr)
meta_loss = 0
num_tasks = 3
for task in range(num_tasks):
# Step 1 : compute one_step weight
input= torch.tensor([(task+1.0)]*2)
f = net(input)
grad = torch.autograd.grad(f, net.parameters(), create_graph=True) # Step 1 Core
fast_weights = list(map(lambda p: p[1] - lr * p[0], zip(grad, net.parameters())))
# Step 2 : compute the loss with one step weight
meta_input= torch.tensor([(task+2.0)]*2)
test_loss = net(input, fast_weights) # Step 2 Core
meta_loss += test_loss
meta_loss /= num_tasks
# optimize theta parameters
meta_optim.zero_grad()
meta_loss.backward()
meta_optim.step()
4. Hessian of a neural network (Hessian Vector Product)
Hessian Matrix $H(\theta)_{N\times N} = \frac{d^2}{d\theta^2} \Big( L(\theta) \Big)$와 Vector $r_{N\times 1}$ 에 대한 Product 연산은
$$ \begin{aligned} H(\theta) \cdot r &= \frac{d^2}{d\theta^2} \Big( L(\theta) \Big) \cdot r \\ &= \frac{d}{d\theta} \Big( \frac{d}{d\theta} L(\theta) \cdot r \Big) \end{aligned} $$
여기서, $r$ 은 $\theta$ 와 관련없는 벡터이므로 Second Derivative 를 계산하는데 영향을 미치지 않습니다.
✅ Step 1. Compute the gradient $\frac{d}{d\theta} L(\theta)$
✅ Step 2. Compute the gradient times vector $\Big(\frac{d}{d\theta} L(\theta) \Big) \cdot r$
net = Net()
params = [p for p in net.parameters() if len(p.size()) > 1]
N = sum(p.numel() for p in params)
print(f"Number of parameters : {N}")
print("Params", params)
# Compute the gardients
input= torch.tensor([(task+1.0)]*2)
f = net(input)
grad = torch.autograd.grad(f, inputs=params, create_graph=True) # Step 1 Core
# Hessian Vector Product
prod = torch.autograd.Variable(torch.zeros(1)).type(type(grad[0].data))
vec = torch.rand_like(prod)
for (g,v) in zip(grad, vec):
prod = prod + (g * v).cpu().sum() # Step 2 Core
prod.backward() # Now the params.grad stores the Hessian
print("----------------------")
print("Hessian Vector Product")
for p in params:
print(p.grad)
5. Implicit Neural Representation
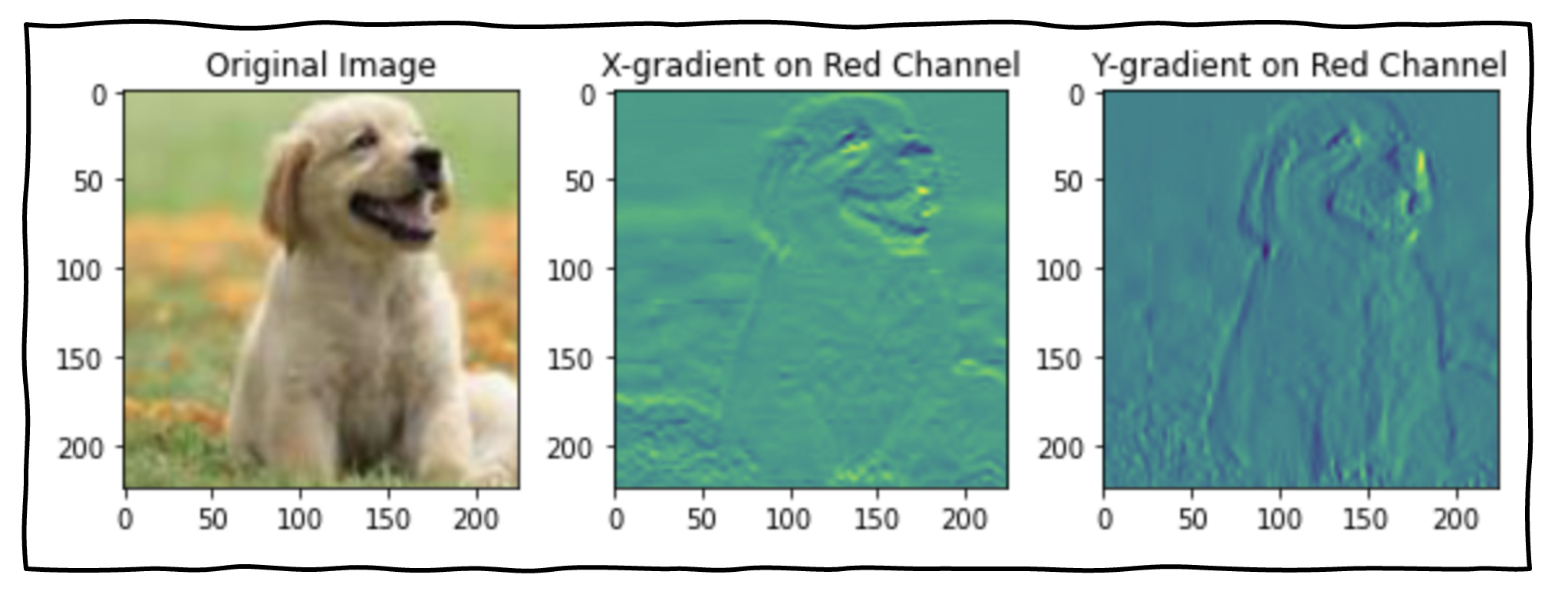
이미지도 함수로 이해할 수 있습니다. 각 픽셀 위치에 대해서 색깔을 예측하는 함수로 말이죠. 그렇기 때문에, 이미지에 대해서도 Gradient 가 있으며, 위 그림처럼 x 방향, y방향에 대해서 빨간색 체널의 Gradient를 구할 수 있습니다. 자세한 내용은 🔖Sobel Filter 를 참조해주세요. 이미지의 Gradient를 신경망으로 Fitting 할 수 있으며, 이 분야를 Implicit Neural Representation 이라고 부릅니다.
1. Original Function : $ f: p(x,y) \rightarrow (r,g,b) $
2. Neural Network Fitting : 위 함수를 근사하는 신경망 $\phi \approx f$
함수를 피팅하는 Objective 는 두 가지 (픽셀값, 그레디언트 유추) 로 나뉩니다.
1. Pixel Fitting : compute the color at pixel position $p'$ $$ \mathcal{L} = ||f(p') - \phi(p')||^2 $$
2. Gradient Fitting : compute the gradient of color at pixel position $p'$
$$ \mathcal{L} = ||\frac{df}{dp}\Big|_{p'} - \frac{d\phi(p)}{dp}\Big|_{p'}||^2 $$
class ImplicitNet(nn.Module):
def __init__(self):
super().__init__()
self.layer = nn.Sequential(
nn.Linear(2, 64), # Input the x,y position
nn.ReLU(),
nn.Linear(64, 3) # RGB prediction
)
def forward(self, x):
x = x.clone().detach().requires_grad_(True)
return self.layer(x), x
net = ImplicitNet()
optimizer = torch.optim.Adam(net.parameters(), lr=1e-4)
# given: position(x,y) --> output: ColorPrediction, position
coordinates = torch.tensor([[0.5, 0.5]])
all_color_prediction, coordinates = net(coordinates)
# Matching the gradient
# assume the ground truth gradient
gt = torch.rand(1, 2)
loss = 0
for channel in range(3): # each R G B
color_predict = all_color_prediction[:, channel]
grad_predict = torch.autograd.grad(color_predict,
coordinates,
create_graph=True)[0] # create_graph makes the optimization possible.
loss+= F.mse_loss(gt, grad_predict)
optimizer.zero_grad()
loss.backward()
optimizer.step()
6. Multiple Backwards
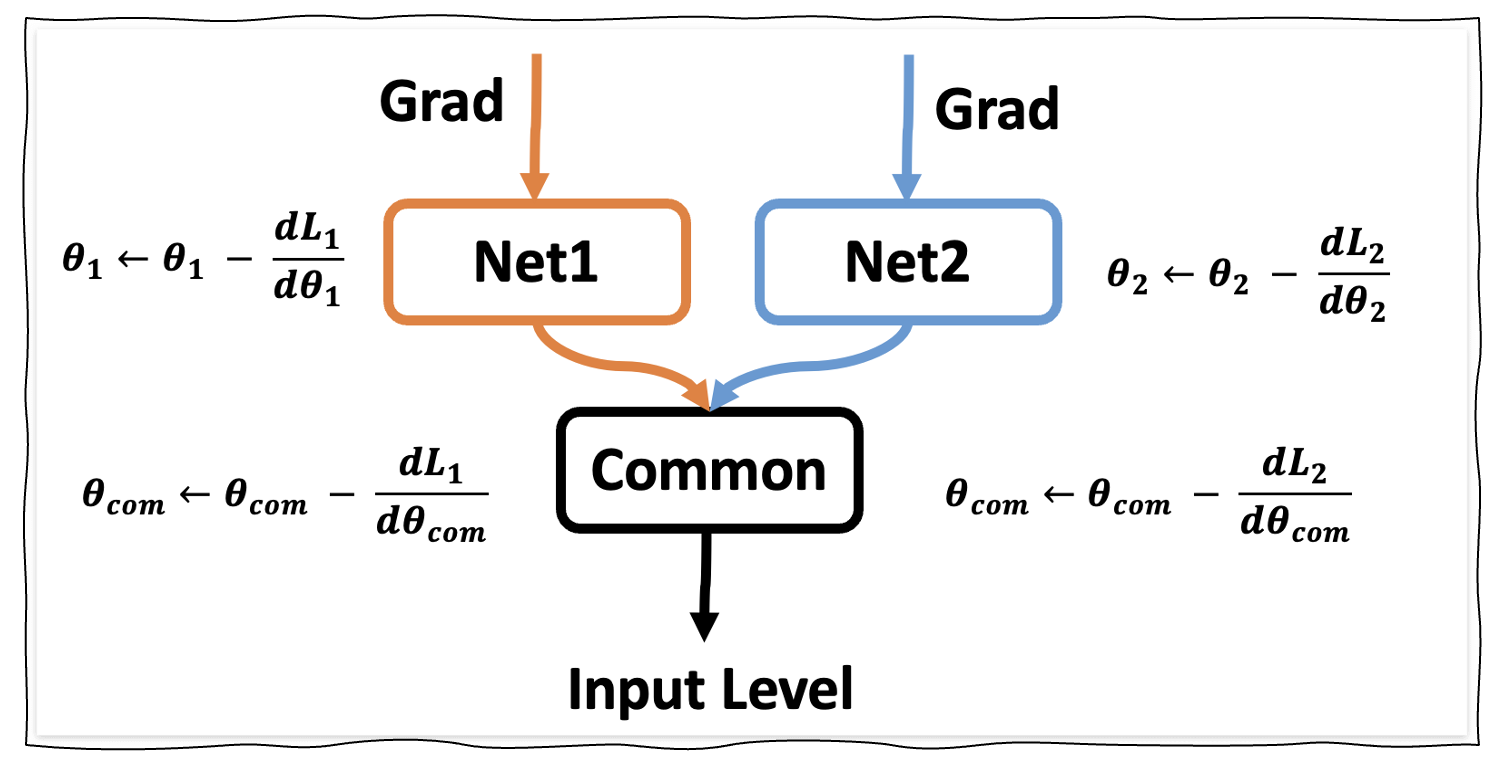
아래 그림과 같이 두 개의 Bracnh 에서 Gradient Descent 를 진행하는 경우,
retrain_graph=True 를 이용하여 backward 한 gradient 를 보존할 수 있습니다.
import torch
import torch.nn as nn
class Net(nn.Module):
def __init__(self):
super().__init__()
self.common = nn.Linear(2, 3)
self.net1 = nn.Sequential(
nn.Linear(3, 5),
nn.ReLU(),
nn.Linear(5,1)
)
self.net2 = nn.Sequential(
nn.Linear(3, 5),
nn.ReLU(),
nn.Linear(5,1)
)
def forward(self, x):
common = self.common(x)
path1 = self.net1(common)
path2 = self.net2(common)
return path1, path2
net = Net()
optimizer = torch.optim.Adam(net.parameters(), lr=1e-4)
input = torch.rand(1, 2)
out_1, out_2 = net(input)
# optimize net1 and common
optimizer.zero_grad()
out_1.backward(retain_graph=True) # Core Code for retaining computational graph
optimizer.step()
# optimize net2 and common (again)
optimizer.zero_grad()
out_2.backward()
optimizer.step()
괜찮은 Use Case가 있다면 공유해주세요 🤗
Reference를 달고 업로드 하겠습니다~!
잘못된 구현도 피드백 해주세요 :)

본문에서 사용된 코드 : https://github.com/fxnnxc/torch_autograd/blob/main/autograd_case_study.ipynb
💛 좋아요 /는 📝포스팅에 💪🏼힘이 됩니다
