[Remark] Implicit Neural Representations with Periodic Activation Functions이 잘되는 이유
[Remark] Implicit Neural Representations
with Periodic Activation Functions 이 잘되는 이유
Implicit Neural Representation 은 데이터에 대한 좌표나 위치를 입력으로 받아서 해당 점의 값을 반환하는 함수를 학습시키는 딥러닝 기법 중 입니다. 이미지나 영상과 같은 시그널 프로세싱에 많이 쓰이며, 신경망에 데이터에 대한 정보를 압축하고 더 나은 표현방법을 학습시켜 데이터의 크기를 줄일 수도 있고, 더 좋은 퀄리티로 복원하는데 사용됩니다. ReLU position encoding과 같이 데이터의 좌표에 시그널 값을 주는 방법이나, Sine activation을 사용하는 방법이 주로 사용됩니다. 이 포스팅에서는 Sine activation이 왜 더 나은 표현 방법인지, 그리고 원 논문의 저자가 제안한 모델은 어떤 강점이 있는지 살펴보겠습니다.
먼저 모델의 구조는 Input X에 대해서 linear transformation + Sine Activation을 반복하는 구조입니다.
$$X_l \rightarrow W_l X_l + b_l \rightarrow \sin(W_l X_l + b_l) \rightarrow W_{l+1}(\cdot)$$
Activation되는 값을 기준으로 살펴보면, 아래 그림에서 첫 번째 열에 해당합니다.
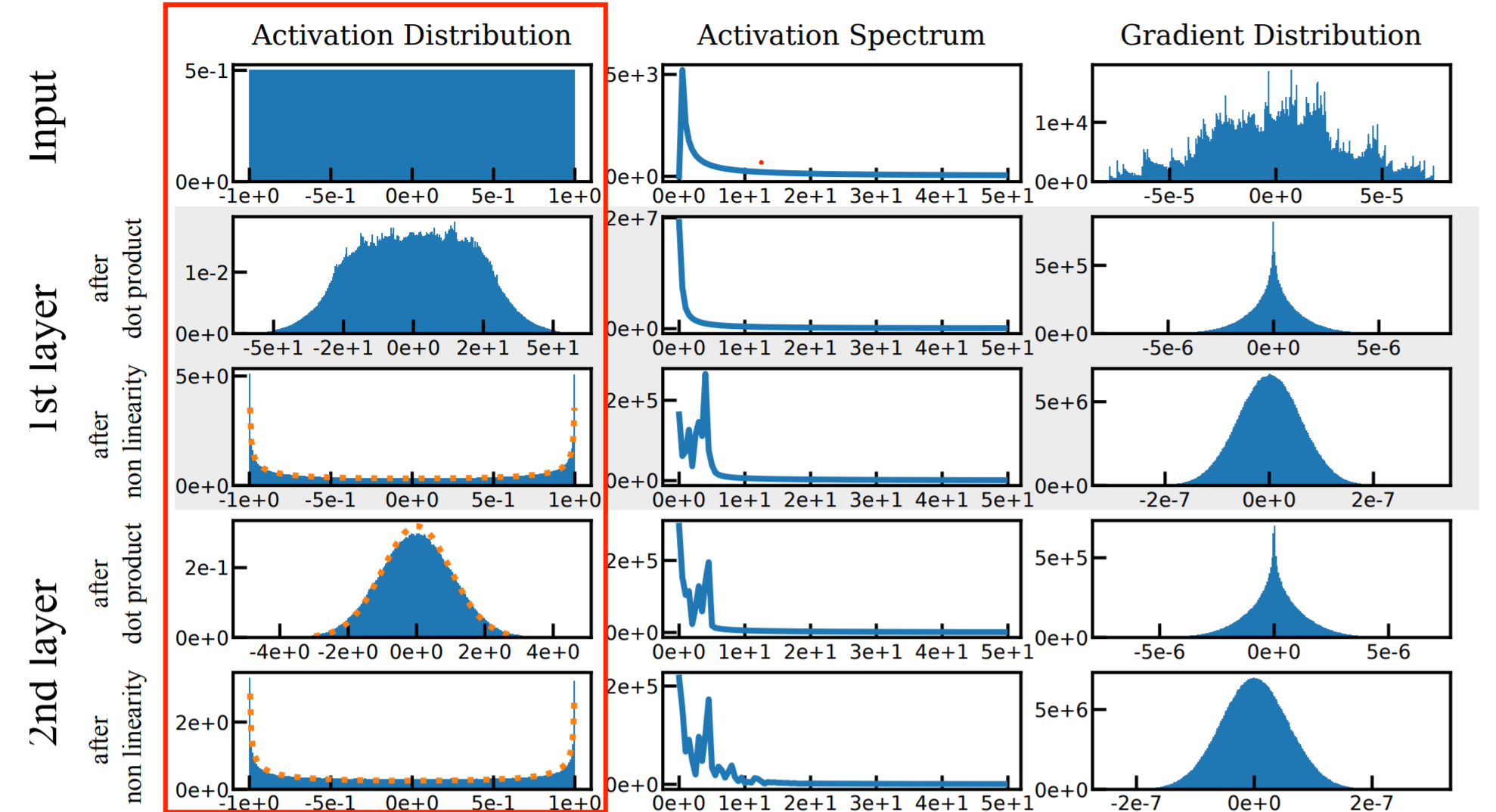
모델의 레이어를 지나감에 따라서 초기값은 1번 분포를 따르며, 나머지는 2,3번을 반복하는 형식으로 분포가 생성됩니다. 논문의 저자는 weight의 분포를 적절한 uniform distribution으로 초기화함으로써, activation의 분포가 standard normal distribution이나 interval이 고정된 arcsin으로 강제시킵니다.
- 초기값: input $X \sim \mathcal{U}(-1,1)$ 을 따르는 초기 상태입니다.
- $W_l X_l \sim \mathcal{N}(0,1)$ # Lemma 1.5
- $sin(W_l X_l + b_l) \sim \text{arcsin}(-1, 1)$ # Lemma 1.6, # Lemma 1.1
Definition (arcsin distribution)
a random variable $X$ by its cumulative distribution function (CDF) $F_X$ such as
$$ X \sim \text{Arcsin} (a,b) , with ~CDF: F_X (x) = \frac{2}{\pi} \text{arcsin} \Big(\sqrt{\frac{x-a}{b-a}}\Big), with ~ b>a $$
Lemma 1.1
Given $X \sim \mathcal{U}(-1,1)$, and $Y = \sin (\frac{\pi}{2} X)$ we have $Y \sim \text{Arcsin} (-1,1)$
Lemma 1.5
Central Limit Theorem with Lindeberg’s sufficient condition: Sn converges to Gaussian distribution
# 이 Lemma로 인해서 Arcsin분포에 weight를 곱하면 standard normal distribution이 됩니다.
🌟 Lemma 1.6
Given a Gausssian distributed random variable $X \sim \mathcal{N}(0,1)$ and $Y = \sin\frac{\pi}{2} X$,
we have $Y \sim \text{Arcsin}(-1,1)$
# 이 Lemma로 인해서 Normal에 sine을 적용하면 arcsin이 됩니다.
Weight $w_0$
기존에 ReLU와 Sine activation이 가지는 장점은 다른 X 값에 대해서 Sine은 동일한 값으로 맵핑을 가능하게 합니다. 예를 들어서, [0,0,1,0,0,1,0,0,1] 과 같이 1이 주기적으로 반복된다면, 1에 해당되는 위치에 대해서 동일한 activation 값을 가지는 모델은 해당 데이터의 좋은 특성을 찾아낼 가능성이 높습니다. 하지만 단순히 sine activation을 하는 것으로는 초기값에 대해서 Sine의 장점을 살리기 어렵습니다. 왜냐하면, X값의 범위가 좁다면, sine의 periodic한 성질이 나타나기전에, one-to-one 맵핑이 될 수 있기 때문입니다. 이에 저자는 omega_0 값을 Sine에 넣기 전에 곱해서 더 다양한 X 값을 얻었습니다.

한 가지 의문점은 omega_0를 곱하는 것과 weight에 omega_0를 곱하는 것의 차이점입니다. 개인적인 의견으로는 omega_0 를 나중에 곱해서 bias term부분을 더욱 증폭시키는데 있는 것 같습니다. 이로부터 Sine함수의 주기성이 사용되는 것 입니다.
피드백 및 커멘트는 언제나 환영입니다. :)