[Meta-Learning] 3. 메타러닝의 데이터셋
Dataset for Meta Learning
Meta Learning 의 Task distribution view에 의하면 Meta Learning 은 Task들에 대한 학습을 통해서 가장 잘 학습하는 알고리즘 $w$를 찾는 것 입니다. 이로부터 새로운 Task에 대해서 빠른 학습, 더 높은 성능을 가지도록 학습합니다.
Meta Learning의 데이터셋은 알고리즘을 찾기 위한 Source Task, 찾은 알고리즘으로 새로운 테스크에 대해서 모델을 훈련시키기 위한 Target Task으로 구분됩니다. 그리고 각각의 M과 Q개의 Task들로 이루어져 있습니다.

Machine Learning
Machine Learning에서는 Dataset에 대해서 다음 Loss를 최소화 하는 파라미터 찾는 것을 목적으로 합니다.
$$
\theta^* \arg \min_\theta \mathcal{L}(\mathcal{D}; \theta, w)
$$
여기서 $w$는 어떤 고정된 알고리즘입니다.
Meta Learning
메타 러닝에서는 task $\mathcal{T} = {D, L}$ 들에 대해서 Loss의 평균을 최소화 하는 알고리즘 $w$를 찾는 것을 목표로 합니다.
$$
\min_w \mathbb{E}_{\mathcal{T} \sim p(\mathcal{T})} \mathcal{L}(\mathcal{D};w)
$$
Task에 대한 distribution에 대해서, 가장 적합한 알고리즘 $w_$를 찾기 위한 데이터와 알고리즘$w$으로부터 모델을 학습시키기 위한 데이터가 다릅니다. 전자는 Source data 후자는 Taregt data 라고 합니다.
Source Data
Source data로부터 가장 적합한 알고리즘을 찾습니다.
$$
w* = \arg \min_w \log p(w| \mathcal{D}_{source})
$$
Target Data
최적의 알고리즘을 이용해서 Target data에 대한 학습을 진행하고, 각 Task 마다 모델 파라미터 $\theta^{*~(i)}$ 를 찾습니다.
$$
\theta^{(i)} = \arg \max_\theta \log p(\theta| w^*, \mathcal{D}_{target}^{train~(i)})
$$
모델 파라미터를 찾으면, 마지막으로 Test data에 대해서 검증을 하면 됩니다.
Bilevel Optimizatino View
다시 정리하자면, data set은 총 3가지로 각 역할은 다음과 같습니다.
- Source data: 최적의 알고리즘 $w*$를 찾습니다.(1)
- Target data: 최적의 알고리즘 $w*$을 이용해서, 모델을 훈련해 파라미터를 찾습니다. (2)
- Test data: 알고리즘과 모델을 검증합니다.
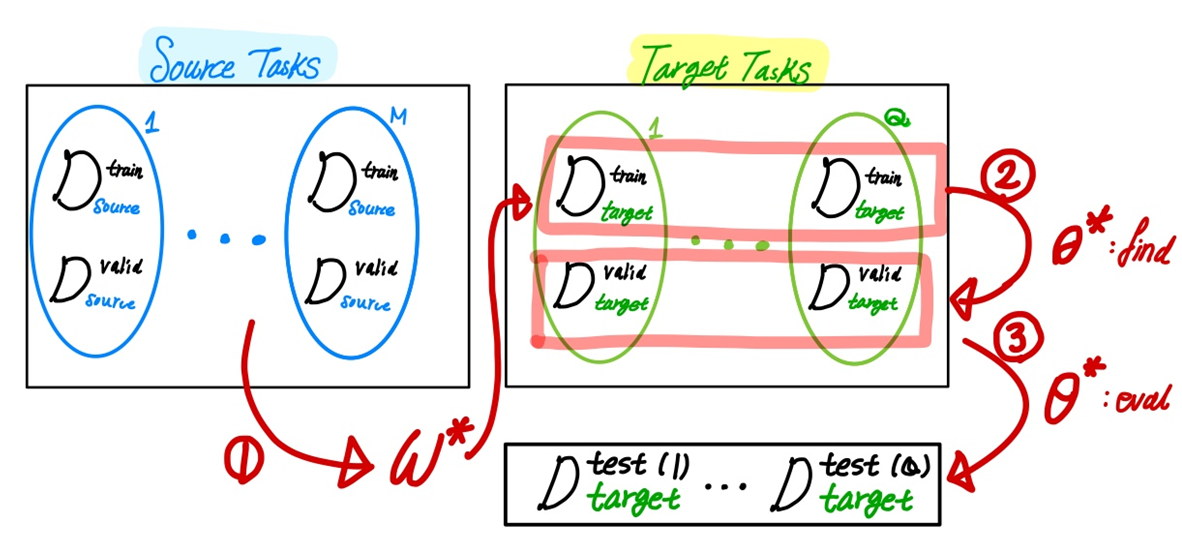
Meta Learning에서는 (1)과 (2)에서 Optimization이 일어나는 것을 볼 수 있고Bilevel Optimization 의 관점에서 식을 적을 수 있습니다.
$$
w* ={ \arg \min}_w \sum_{i=1}^M \mathcal{L}^{meta}(\theta^{*~(i)} (w), w, \mathcal{D}_{source}^{val~(i)})
$$
$$
\text{s.t.~} \theta^{*(i)} (w) = {\arg \min}_\theta \mathcal{L}^{task}(\theta, w, \mathcal{D}_{source}^{train~(i)})$$
메타러닝이 지니는 의미 learning to learn 의 의미는 단순히 최적의 모델을 찾는 것이 아니라, Source Data에 대해서 이를 가장 잘 학습시킨 알고리즘 $w*$를 찾는데 있습니다. Meta Learning은 (데이터, Loss) Pair로 하나의 테스크를 정의하며 학습방법인 알고리즘으로 새로운 Task에 대해서 빠르고, 더 높은 성능으로 학습시키는 것을 목표로 합니다. 다음에는 이와 관련된 예제에 대해서 좀더 자세히 살펴보겠습니다. 🤗🤗