Inference
데이터에 대한 관찰로 사후에 일어날 일을 예측을 할 수 있습니다. 사건에 대해서 예측을 위해서는 발생확률을 알아야 합니다. Frequentist와 Bayesian의 Posting에서는 데이터가 아닌, 모델에 대한 추론을 이야기하려 합니다. 두 관점은 접근법이 다르기 때문에 바탕이 되는 철학이 다릅니다.
맨날 싸운다는 소문이...
예를 들어서 1부터 6이 적힌 울퉁불퉁한 주사위를 굴려서 1이 나오는 사건을 생각해봅시다.
1이 나오는 확률에 대해서 알지 못하기 때문에, 몇 번의 관찰 이후에 1이 나올 확률을 예측해야 합니다.
Frequentist
Frequentist는 모델에 대한 참값이 있으며, 임의로 발생하는 것은 데이터라고 생각합니다.
모델의 파라미터에 대한 참값이 있으며, 데이터가 랜덤으로 주어지는 것 입니다. 따라서 데이터에 대해서 이를 가장 잘 설명할 수 있는 단 하나의 모델을 찾아야 합니다.
모델$f$의 파리미터 $\theta$와 데이터 $D$에 대해서 해당 사건이 일어날 확률은 다음과 같이 적을 수 있습니다.
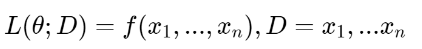
여기서 만일 관찰된 얘들이 독립적이라면(서로 영향을 끼치지 않는다면) 좀더 깔끔하게 적을 수 있습니다.
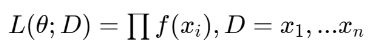
여기서 Frequentist는 모델에 대한 파라미터(세타)를 찾기 위해서 Likelihood를 세타 대해서 편미분하고 값이 가장 커지는 세타를 찾습니다. Frequentist는 보다 직관적이며, 현상을 최적으로 설명하는 모델 파라미터 세타를 찾습니다. 추가적으로 예측에 대해서 P-value를 따져서 모델이 적합한지 평가하는 것도 Frequentist의 관점이 됩니다.
울퉁불퉁 주사위를 100 번 던져서, 1이 나올 확률을 (예를 들어) 30/100 이라고 구했다면 Frequentist입니다. 걷으로 보기에는 그냥 경우의 수로 계산한 거지만, *30/100 확률이 Likelihood를 최대화하는 값입니다. (=) *
Bayesian
Bayesian에서는 데이터가 참이며 이를 가장 잘 설명하는 모델을 선택합니다. 주사위 모델에 대한 참값이 있다는 Frequentist와는 달리, Bayesian에서는 주사위 모델에 대한 다양한 모델이 있으며 가장 잘 설명할 수 있는 것을 선택합니다.
예를 들어서 32번을 던졌을 때, 1이 2, 4, 8, 16번 나왔다고 한다면, Frequentist는 데이터를 가장 잘 설명하는 2의 지수승 모델을 선택할 수 있지만, Bayesian에서는 해당 모델이 데이터를 가장 잘 설명하지만, 모델이 정답은 아니니까 가능성이 높은 다른 모델도 고려해보자. 이렇게 이야기 합니다. 그 이유는 바로 다음 식 때문입니다.
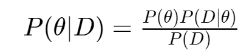
Bayesian에서는 Conditional Probability의 순서를 Bayesian Rule에 의해서 바꿀 수 있기 때문에 서로 다른 내용을 나타내는 좌우변의 값이 같다는 것을 알 수 있습니다.
좌 : 데이터를 설명하는 모델에 대한 확률
우 : 모델에 대한 확률(선호도) 와 모델에 의한 데이터의 설명력의 곱
따라서 주어진 데이터에 대한 모델의 확률은 모델의 선호도와 모델에 의한 데이터의 확률로 나타낼 수 있습니다.
여기서 모델의 선호도란 데이터를 보기 전에 모델이 얼마나 선호되는지 입니다. 주사위 모델에서 주사위가 2의 지수승을 나타낸다고 생각하기보다 모두 동일한 확률이라고 생각하는게 더 선호도가 높습니다. (사람마다 다를 수 있겠죠)
여기서 Bayesian의 문제가 나타납니다. 반드시 모델에 대한 사전확률을 알아야 하기 때문에, 이를 구해야만 합니다.
보통은 샘플링을 통해서 구한다고 합니다. 결론적으로 확률이 최대가 되는 세타를 다음과 같은 방식으로 찾습니다.
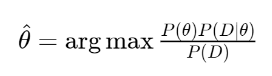
결론
두 가지 중에서 우위를 지니는 것은 없지만, 최근에 딥러닝, 머신러닝이 발달하면서 Bayesian이 굉장히 많이 쓰이고 있습니다. 저 같은 경우는 모델에 대한 사전확률이 주어져서 모델의 선호도를 결정할 수 있다는 것이 Bayesian의 매력인 것 같네요.

- 커맨트나 오류 수정은 언제나 환영입니다!
'데이터분석' 카테고리의 다른 글
| 다중공선성은 모델에 어떤 영향을 미치는가? (0) | 2020.08.12 |
|---|---|
| Biased Estimation, Unbiased Estimation (0) | 2020.08.04 |
| Spark 기본 설명 (0) | 2020.07.30 |
| [Warehouse] Pandas Skills (0) | 2020.07.18 |
| [Word Cloud] Mask를 이용한 Word Cloud + Python (0) | 2020.07.17 |
